サレジオ学院進学館はフリーダムオンラインが運営する、サレジオ学院合格をめざす生徒の学校別進学コースです。
当館は、オンライン指導(サレジオ学院個別ワークス)による個別指導システムです。
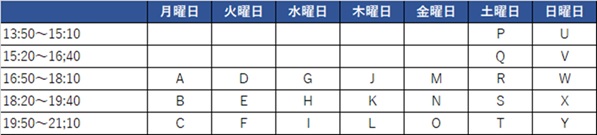
授業は、それぞれの生徒に向けて指導プログラムを組んで行います。サレジオ学院合格に向けて、現状の分析と科目対策を講師が策定して、合格までのプロセスを明確にします。授業時間は自由選択制ですので、タイムテーブルの中から都合の良い時間を選択できます。
指導は、講師の指示にしたがって問題を解き、その答え合わせをしてわからない問題は講師が解説し、さらに理解を深めていきます。また、WEBワークスの学校別バインダーを使って、不得意科目や類題の演習も合わせて行います。
標準的なプログラムとしては、6年生の1年間を前期と後期に分けます。
【前期指導】
過去問の研究とそれぞれの生徒の理解状況の確認になります。過去問を解きながら生徒の得手不得手を講師がチェックし、不足している部分は学校別バインダーやWEBワークスの中から練習します。
【後期指導】
後期は、2学期を概ね想定していますが、過去問の他にオリジナルのそっくりテストを演習し、中大横浜の傾向対策を万全にすると共に、細かいミスがでないように、確実な得点をめざす練習。を続けていきます。また知識力のチェックを行い、確実な知識問題の得点を狙っていきます。
【無料体験申込み】
無料体験授業を受け付けています。以下のフォームからお申込みいただけます。
【学習相談申し込み】
テレビ電話ZOOMを使った学習相談を承っております。以下のフォームからお申込ください。
